

My university professor once said to us: Maths as a subject in general can be understood in 3 ways. The algebra, the visualization and the proof. In IB maths, proof is generally not a heavy topic, but the first 2 should ring a very clear bell.
When a new topic is introduced, your Maths teacher will first teach you about a rigorous definition of key terms. Such as in Calculus, differentiation from first principle is defined as

You as a student should be quite confused by its meaning. But hopefully your teacher will continue to explain the underlying interpretation and visualization. Maybe with a graph like this.
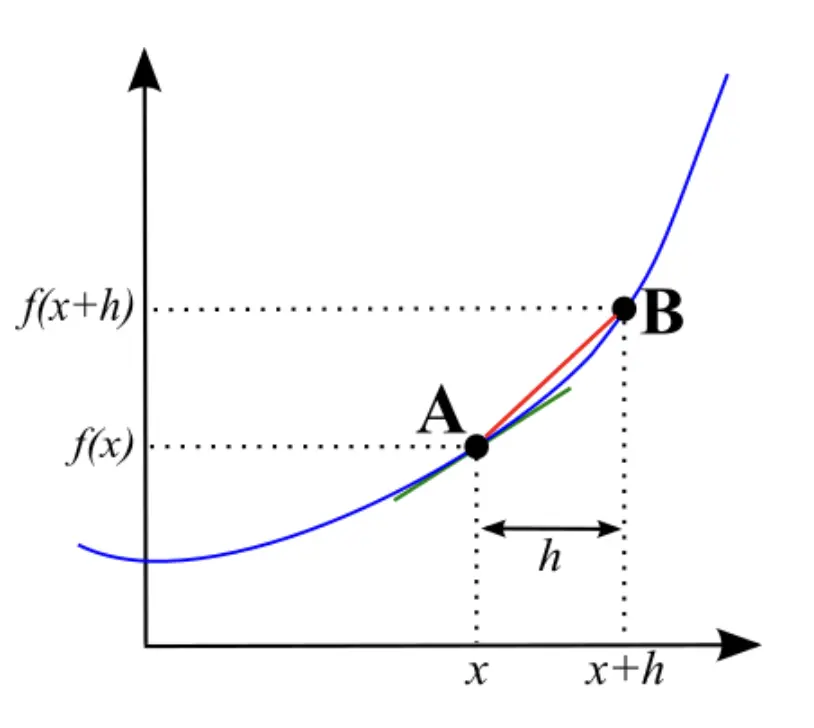
Together with the visualization and the algebra, you should both see and think that when h becomes infinitely small, the ‘rise’ over ‘run’ will eventually be the same as a line equation.
IB maths does not heavily involve the use of rigorous proofs. But even without a rigorous proof of the first principle, your intuition of the graph and the understanding of the algebra should give you a deep appreciation of Calculus.
Differentiation in calculus is just an example of how you can greatly benefit from having a deeper understanding using the algebra and visualization. But it can be also extended to other topics. But this also broadly summarizes the objectives of your IB exam. When an examiner makes a question, they will think about how this question will be tricky in its algebraic manipulation, or how it will require a visualization of how things behave or both. As a HL student, you will be tested on these skills by 3 separate exams.
The Basics: Exam Structure
- Paper 1: No calculator. Focuses on algebra, proofs (induction/direct), and precise manipulation. 2 hours, 110 marks.
- Paper 2: Calculator allowed. Involves extended questions and applications where technology is essential. 2 hours, 110 marks.
- Paper 3: HL students only. A deep-dive into one advanced topic (such as calculus, statistics, or discrete mathematics). 1 hour, 55 marks.
- Weighting: Paper 1 = 30%, Paper 2 = 30%, Paper 3 = 20%, IA = 20%.
Most of the content covers only what you understood about the content matter. With a few questions every now and then requiring a deeper understanding. Luckily, if you have done 5+ past papers, and you have checked through the answers. You should have a very clear pattern of what the questions should look like. And about 60-80% of your test will have the same style of the past papers.
If you’re wondering how this translates to final outcomes, see our explainer on how IB grading works and our guide to IB to ATAR conversion.
Exam techniques and how to revise for exam
Understand Concepts, Don’t Just Memorize
- Focus on why formulas work, not just what they are. It’s also useful to try write out the formula without looking at the formula booklet, not because you have memorized, but because you understand what each component of the formula means so you can derive it in your head automatically.
For a research-backed boost, see evidence-based study strategies and build a routine with a solid study plan.
Estimate or Sense-Check Answers (sanity check)
- Ask: “Does this value make sense?” For example, if your answer ends up with negative inside a square root, it’s obviously wrong. Another classic one is area under the curve. When you apply integration to find area under the curve, the value should never be negative!
Use the Question for Clues
- If it says “show that … = 4xyz,” you already know the right hand side. Look closely at how it’s presented so you can get a hint about how to manipulate the lefthand side to arrive the right hand side.
Learn your IB command terms—they tell you exactly what the examiner expects.
Skip and Return
- If you’re stuck for 2–3 minutes, move on. The order of questions on your exam is typically by the order of topic and not by difficulty. So some questions can be deceivingly hard from early on.
Show Every Step Clearly
- You probably have heard you teacher saying this a thousand times, but this is a big one. You should look closely at the mark scheme to understand what kind of ‘middle working’ can get you a partial mark. Even if your final answer is wrong, method marks can still get you partial mark.
Good notes help here—see our guide to effective note-taking.
‘Hence’
- If a following up question has ‘hence’, always always refer back to the previous question for hint. Definitely use the parts given by the previous question.
Common Mistakes for Maths AA HL
- Relying too heavily on the calculator without interpretation.
- Spending too much time on one difficult question.
- Misreading word problems by rushing through them.
Final Advice for Maths AA HL
- If you are stuck, write down what you know. You can potentially see some hint from the stuff you wrote down on paper.
- Expect Paper 3 to feel unfamiliar; regular practice makes it manageable.
- Do not neglect your Internal Assessment, as it makes up 20% of your grade.
- Confidence comes from consistent practice, not last-minute cramming.
If you need targeted help, here’s why one-to-one tutoring works.
Resources That Help for Maths AA HL
- Online resources: Revision Village, Mitch Campbell’s IB Mathematics videos.
- Reddit: subreddits like ‘learnmath’ has some interesting discussion on Maths. If you search a confusing topic from your study, you should find plenty of discussions on it.
- Chatgpt: don’t have it do the Maths question for you. In fact it’s quite dumb when solving a numeric problem with plenty of errors. Instead, ask the bigger picture questions such as ‘what’s the intuition behind integration?’





